Tablut AI

A funny challenge!

Tablut is an ancient Lappish board game and its very well defined rules make it a perfect test field for a search algorithm.

As part of my Master’s degree exam in Fundamental of AI, my team and I developed the Nega-Max algorithm with an alpha-beta pruning, which is able to autonomously play Tablut game. We also designed a Genetic Algorithm to find the best evaluation function .

Let’s have a look at the ancient Tablut game and at the structure of our algorithm, with a short overview of the main theoretical concepts.

---

The game

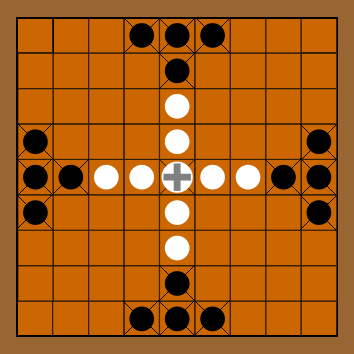
Tablut is a two-players game which is played on a 9×9 board. The two players, black and white, have two different goals:

• the white player has to bring his king in one of the escape squares;
• the black player, who has no king, tries to capture the opponent king.

The initial configuration has the white king in the center of the board with 8 white soldiers to protect him. The 16 black soldiers are placed in the camp squares

The white player starts the game. Each piece on the board can move vertically or horizontally by any given number of vacant squares. To capture an opponent pawn, the player has to catch it between two of her/his pawns set in a row or column.

The game ends as soon as the white king escapes or is captured.

---

A bit of theory

Tablut is a so called zero-sum game: each player’s gain or loss is perfectly balanced by the loss or gain of the other player, therefore by adding all the participants gains and subtracting all their losses, we get exactly zero. In Tablut this concept can be formulated in terms of advantage given by the current board configuration which can be encoded in a designed objective function. The two players have two complementary objective functions.

Tablut is also a perfect information game, which means that the opponents have a full knowledge about the current game configuration and there is no hidden information (an example of games with hidden information is card games).

Thanks to its characteristic, a Tablut game can be seen as the generation of a search tree with the starting configuration as root and the final configurations as leaves (fail, success or draw leaves).

A very common algorithm used to traverse the search tree of a game like Tablut is the Mini-Max Algorithm. This algorithm is exploited in fields such as AI, decision theory and statistics to minimize the possible loss in a worst case scenario.

Let’s call the two players maximizer (MAX) and minimizer (min). Given a configuration, the algorithm provides the best next move for MAX assuming that min plays at its best. The focus of Mini-Max is not on the entire path to the success leaf, but only on the next move.

The Mini-Max algorithm has several disadvantages which make it useless for complex games: its time complexity grows exponentially with the maximum depth of the search tree.

To overcome these problems, there exist several improvements of Mini-Max algorithm and we decided to implement the so called Nega-Max algorithm with alpha-beta pruning technique and transposition tables.

---

The algorithm: Nega-Max with alpha-beta pruning

As a first step, we built the game structure by developing the rules and the winning conditions.

Then we started thinking about the possible development of the algorithm and we decided to implement:

• the Nega-Max algorithm which exploits the zero-sum property of Tablut;
• the alpha-beta pruning techinque which reduces the number of evaluated nodes during the search;
• the Trasposition Table which avoids re-evaluating an already seen configuration.

Here is the pseudocode of the algorithm taken from Wikipedia (the implementation is on Github).

function negamax(node, depth, α, β, color) is
    alphaOrig := α

    (* Transposition Table Lookup; node is the lookup key for ttEntry *)
    ttEntry := transpositionTableLookup(node)
    if ttEntry is valid and ttEntry.depth ≥ depth then
        if ttEntry.flag = EXACT then
            return ttEntry.value
        else if ttEntry.flag = LOWERBOUND then
            α := max(α, ttEntry.value)
        else if ttEntry.flag = UPPERBOUND then
            β := min(β, ttEntry.value)

        if α ≥ β then
            return ttEntry.value

    if depth = 0 or node is a terminal node then
        return color × the heuristic value of node

    childNodes := generateMoves(node)
    childNodes := orderMoves(childNodes)
    value := −∞
    for each child in childNodes do
        value := max(value, −negamax(child, depth − 1, −β, −α, −color))
        α := max(α, value)
        if α ≥ β then
            break

    (* Transposition Table Store; node is the lookup key for ttEntry *)
    ttEntry.value := value
    if value ≤ alphaOrig then
        ttEntry.flag := UPPERBOUND
    else if value ≥ β then
        ttEntry.flag := LOWERBOUND
    else
        ttEntry.flag := EXACT
    ttEntry.depth := depth	
    transpositionTableStore(node, ttEntry)

    return value

---

Evaluation Function and Genetic Algorithm

A crucial element of any Mini-Max variant is the evaluation function that estimates the heuristic value of a non-terminal node. The evaluation function has to be carefully designed in order to find a balance between the algorithm efficiency and its optimality.

We designed our evaluation function looking at:

• the number of black and white pieces;
• the king position.

The king position is evaluated according to the number of reachable escapes, the number and color of the closest soldiers, and the physical position on the board.

Each element of the evaluation function is weighted, but how can we tune the weights?

We decided to use a very well known population-based method: the Genetic Algorithm (GA), which is inspired by the process of natural selection.

Our GA has a population of 200 agents (100 white players and 100 black players). Each player has a random weights configuration and at each epoch we select the best individuals using a tournament selection with the number of winning as fitness function. The fitness function also includes a time-out parameter to fix a maximum game duration.

The offsprings are generated through a two-point crossover with a low mutation probability. The new population for each color is composed by the best 50 old agents and the best 50 new agents (truncation selection).

At the end we obtain the best white and black weights configuration according to the fitness function.